8.3 Uzawa’s method

We now move to a different kind of algorithm, which exploits duality. The main idea of Uzawa’s method is to apply the projected gradient method to the dual problem.

First let us start with a reminder from Chapter 7. The primal problem we consider has the form

and the associated dual problem is

where $L$ is the Lagrangian

Principle¶

The dual problem is a constrained optimization problem with non-negativity constraints $\lambda \geq 0$ on Lagrange multipliers associated to inequality constraints. It turns out that projection onto the non-negative orthant is explicit and efficient:

Since the dual problem is a maximization problem, we can use projected gradient ascent on the Lagrangian $L(x^{(k)}, \lambda, \nu)$ for a given $x^{(k)}$. The principle is as follows:

• given current $(\lambda^{(k)}, \nu^{(k)})$, compute $x^{(k+1)} \in \argmin L(x, \lambda^{(k)}, \nu^{(k)}))$

• then update the Lagrange multipliers by a step of gradient ascent. Since the Lagrangian is separable in $(\lambda, \nu)$

  • $\lambda^{(k+1)}_i = \max(0, \lambda^{(k)}_i + \alpha_k f_i(x^{(k+1)}))$, $i=1, \ldots, m$ (projected gradient ascent)

  • $\nu^{(k+1)}_i =\nu^{(k)}_i + \beta_k h_i(x^{(k+1)})$, $i=1, \ldots, p$ (gradient ascent)

and so on until convergence.

Under suitable conditions, such algorithm is shown to converge to a saddle-point of the Lagrangian (hence it yields primal and dual optimal points).

Examples¶

1D example¶

Consider the following problem

with trivial solution $x^\star = 2$. The Lagrangian is $L(x, \lambda) = x^2+ \lambda (x-2)(x-4) = (1+\lambda)x^2 -6\lambda + 8$.

For fixed $\lambda \geq 0$, $\argmin_x L(x, \lambda) = 3\lambda/(1+\lambda)$. Hence Uzawa’s algorithm with fixed step size $\alpha_k = \alpha$ reads

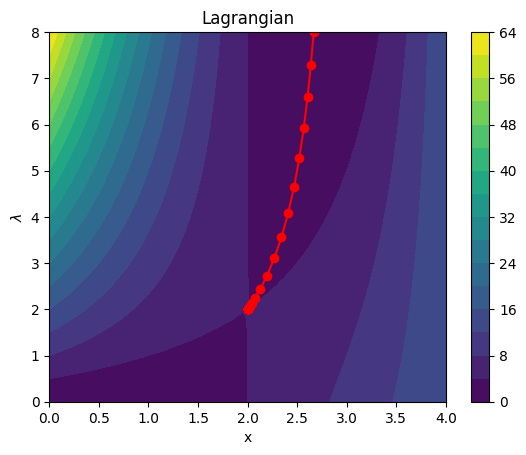
and so on, until convergence. Here’s a small example of trajectory on the Lagrangian, for $\lambda^{(0)} = 8$.

Source

import numpy as np
import matplotlib.pyplot as plt

def f0(x):
    return x**2

def f1(x):
    return (x-2)*(x-4)

def L(x, l):
    return f0(x) + l*f1(x)

def uzawa(l0, alpha=0.1, niter=10):


    lks = [l0]
    xks = []
    for k in range(niter):
        xks.append(3*lks[k]/(1+lks[k]))
        lk1 = np.maximum(0, lks[k]+ alpha*f1(xks[-1]))
        lks.append(lk1)
    return xks, lks

xks, lks = uzawa(8, alpha=.8, niter=50)
x = np.linspace(0, 4)
l = np.linspace(0, 8)
xx, ll = np.meshgrid(x, l)

plt.contourf(x, l, L(xx,ll), levels=20)
plt.xlabel('x')
plt.ylabel('$\lambda$')
plt.colorbar()
plt.title('Lagrangian')

plt.plot(xks, lks[:-1], '-o', c='r', )

We clearly observe converge to the optimums $\lambda^\star = 2$ and $x^\star = 2$.

Non-negative least squares¶

Let us write Uzawa’s iterates for the following problem

where $A$ is full column rank.

The Lagrangian for the problem is $L(x, {\lambda}) = \frac{1}{2}\Vert y - Ax\Vert_2^2 - {\lambda}^\top x$ with gradient with respect to $x$ given by $\nabla_{x} L(x, {\lambda}) = A^\top (Ax-y) -{\lambda}$. Therefore we have the iterations

until primal and dual convergence.