2.3 Convexity and uniqueness of solutions
Convexity is a key tool to study uniqueness of solutions in optimization.
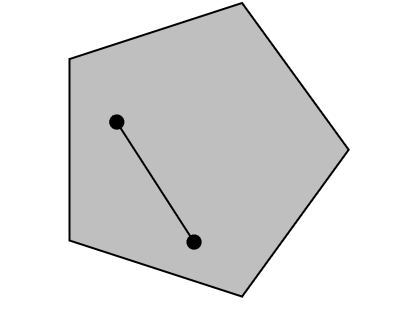
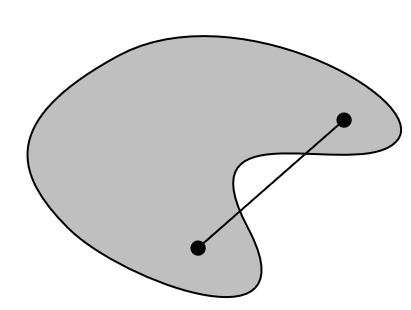
Convex sets ¶ A set C \mathcal{C} C x 1 , x 2 ∈ C {x}_1, {x}_2 \in \mathcal{C} x 1 , x 2 ∈ C θ ∈ [ 0 , 1 ] \theta \in [0, 1] θ ∈ [ 0 , 1 ]
θ x 1 + ( 1 − θ ) x 2 ∈ C \theta {x}_1 +(1-\theta){x}_2 \in \mathcal{C} θ x 1 + ( 1 − θ ) x 2 ∈ C Equation (1) x 1 , x 2 ∈ C {x}_1, {x}_2 \in \mathcal{C} x 1 , x 2 ∈ C x 1 {x}_1 x 1 x 2 {x}_2 x 2 C \mathcal{C} C
Convex functions ¶ Let Ω ⊆ R n \Omega \subseteq \mathbb{R}^n Ω ⊆ R n f : Ω → R f:\Omega \rightarrow \mathbb{R} f : Ω → R Ω \Omega Ω x 1 , x 2 ∈ Ω {x}_1, {x}_2 \in \Omega x 1 , x 2 ∈ Ω θ ∈ [ 0 , 1 ] \theta \in [0, 1] θ ∈ [ 0 , 1 ]
f ( θ x 1 + ( 1 − θ ) x 2 ) ≤ θ f ( x 1 ) + ( 1 − θ ) f ( x 2 ) f(\theta{x}_1 + (1-\theta){x}_2) \leq \theta f({x}_1) + (1-\theta)f({x}_2) f ( θ x 1 + ( 1 − θ ) x 2 ) ≤ θ f ( x 1 ) + ( 1 − θ ) f ( x 2 ) and strictly convex if the inequality is strict.
Useful characterization results for convex functions ¶ In the following we give two practical theorems to characterize the convexity of functions f : Ω → R f:\Omega \to \mathbb{R} f : Ω → R Ω ⊆ R n \Omega \subseteq \mathbb{R}^n Ω ⊆ R n f ∈ C 1 f \in C^1 f ∈ C 1 f ∈ C 2 f\in C^2 f ∈ C 2 Ω = R n \Omega = \mathbb{R}^n Ω = R n
Let f : R n → R f:\mathbb{R}^n \rightarrow\mathbb{R} f : R n → R
f f f R n \mathbb{R}^n R n
For all x , y ∈ R n {x}, {y} \in \mathbb{R}^n x , y ∈ R n f ( y ) ≥ f ( x ) + ∇ f ( x ) ⊤ ( y − x ) f({y}) \geq f({x}) + \nabla f({x})^\top ({y}-{x}) f ( y ) ≥ f ( x ) + ∇ f ( x ) ⊤ ( y − x )
For all x , y ∈ R n {x}, {y} \in \mathbb{R}^n x , y ∈ R n ( ∇ f ( y ) − ∇ f ( x ) ) ⊤ ( y − x ) ≥ 0 \left(\nabla f({y}) - \nabla f({x})\right)^\top \left({y}-{x}\right) \geq 0 ( ∇ f ( y ) − ∇ f ( x ) ) ⊤ ( y − x ) ≥ 0
The equivalence is preserved for strict convexity, with x ≠ y {x} \neq {y} x = y
A classical counter-example is f : R → R f:\mathbb{R} \to \mathbb{R} f : R → R f ( x ) = x 4 f(x) = x^4 f ( x ) = x 4 Definition 2 Theorem 1 f ′ ′ ( x ) = 12 x 2 f''(x) = 12x^2 f ′′ ( x ) = 12 x 2 x = 0 x = 0 x = 0
Uniqueness of solutions in optimization ¶ Consider the following optimization problem
minimize f 0 ( x ) subject to x ∈ Ω \begin{array}{ll}
\minimize& f_0({x})\\
\st & x \in \Omega
\end{array} minimize subject to f 0 ( x ) x ∈ Ω The following theorem is very useful.
Proof
Exercise! (hint: by contradiction)
Theorem 3 p ⋆ p^\star p ⋆
minimize e x subject to x ∈ R \begin{array}{ll}
\minimize& e^x\\
\st & x \in \mathbb{R}
\end{array} minimize subject to e x x ∈ R admits no solution (p ⋆ = 0 p^\star = 0 p ⋆ = 0 f 0 f_0 f 0
By definition, f f f − f -f − f
Optimization problems of the form
minimize f 0 ( x ) subject to x ∈ Ω \begin{array}{ll}
\minimize& f_0({x})\\
\st & x \in \Omega
\end{array} minimize subject to f 0 ( x ) x ∈ Ω where f 0 f_0 f 0 Ω ⊆ R n \Omega\subseteq \mathbb{R}^n Ω ⊆ R n convex optimization problems .
It is one of the most successful field in numerical optimization.
the special (and important!) case of quadratic functions
f ( x ) = x ⊤ Q x + p ⊤ x + r ( with Q = Q ⊤ ) f(x) = x^\top {Q}x + {p}^\top x + {r} \qquad (\text{with }{Q} = {Q}^\top) f ( x ) = x ⊤ Q x + p ⊤ x + r ( with Q = Q ⊤ )